Hoe ‘normaal’ is de wereld, veronderstel een blikopener?
Statistiek is ontegenzeggelijk een zeer krachtig instrument, alleen zoals met zoveel mooie elegante middelen nodigt zij helaas ook veel mensen uit om haar toe te passen waar het niet gepast is.
100% correlatie tussen zin en onzin
Correlaties kunnen een hypothese bevestigen, maar niet andersom.
Zo kan het zijn dat we, na enig ‘logisch’ denkwerk, vermoeden dat er een verband bestaat tussen de calorie-inname van iemand en zijn gewicht. Onze hypothese laat zich in een simpel experiment bevestigen door aan te tonen dat er een duidelijke correlatie tussen de twee is.
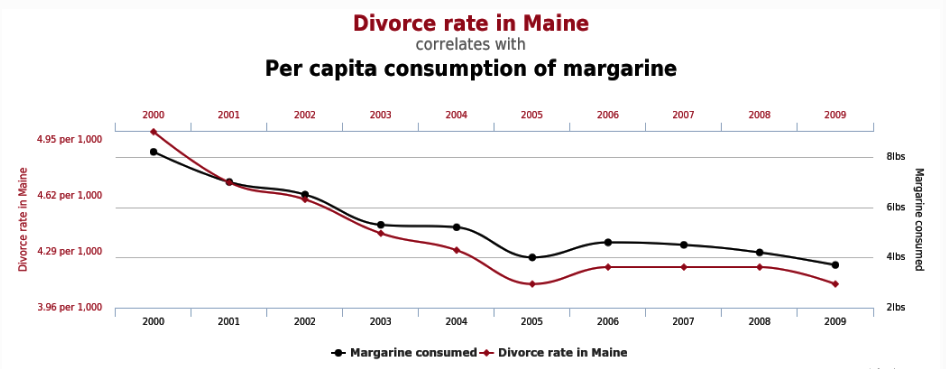
Echter, als we het omdraaien, dan kunnen we ook heel simpel laten zien dat er een heel sterk statistisch verband bestaat tussen de toename van het aantal telefoonaansluitingen en de toename van kanker, zijnde dat ze allebei een lineair stijgend patroon laten zien in de tijd. Immers als zowel het aantal telefoonaansluitingen als het aantal kankergevallen in de tijd lineair stijgt, laten ze beide als we ze aan elkaar correleren ook een sterk verband zien. Er is zelfs een aparte website met voorbeelden van absurde correlaties, getuige het hieronder gepresenteerde voorbeeld dat doet vermoeden dat in de Amerikaanse staat Maine de kans op een echtscheiding afneemt als u minder margarine eet.
Extremistan en mediocristan
In zijn boek De Zwarte Zwaan, dat verplichte kost zou moeten zijn voor veel studies, universiteiten en hogescholen, presenteert Taleb twee verschillende werelden. De ene wereld, mediocristan, is een beperkte wereld waar het gemiddelde en de statistiek werkt (de wereld van Gauss) en de andere, Extremistan, de wereld waar het werken met gemiddelden en statistiek tot totaal onzinnige conclusies leidt.
Het verschil laat zich het best presenteren aan de hand van een gedachte-experiment.
We kiezen willekeurig de eerste 1.000 mensen die we tegenkomen en meten hun gewicht en lengte. De uitkomst is dat een gemiddeld mens 1,71 meter is met een gemiddeld gewicht van 60 kg (n=1000). Nu mag u de gehele wereld afzoeken en zowel de zwaarste als de langste persoon toevoegen aan de populatie (stel 300 kg en 3 meter, n=1002). Beiden hebben een bijna verwaarloosbaar effect op het gemiddelde. Een perfect voorbeeld van een normaal verdeelde wereld: mediocristan.
Nu kiezen we dezelfde 1.000 mensen en tellen hun gemiddeld jaarinkomen op. We mogen verwachten dat dit in de buurt van een modaal inkomen van € 32.000 per jaar uitkomt. Als we nu het jaarinkomen van de rijkste man ter wereld toevoegen (Bill Gates), dan stijgt het gemiddeld inkomen van de nieuwe populatie zodanig dat we ineens duizend-en-één miljonairs hebben: Extremistan!!!
Veronderstel ‘een blikopener’
Een technocraat, een theoretisch natuurkundige en een econoom/statisticus spoelen samen met een blikje bonen op een onbewoond eiland aan. Gedreven door honger steken de heren de koppen bij elkaar om zich te beraden over een mogelijke manier om het blikje te openen.
De techneut denkt direct aan een hefboom door met een geknakte tak van een boom voldoende druk te kunnen zetten om het blikje met mechanisch geweld te kraken. De theoretisch natuurkundige overweegt om de lenswerking van een plas water te gebruiken om met het brandpunt en een hoop geduld een gat in het blikje te branden om zo toegang tot de bonen krijgen. Tot slot start de econoom/statisticus zijn betoog met . . . . “veronderstel een blikopener!”
Als grap is het bovenstaande verhaal misschien minder geslaagd, maar als demonstratie van wat op grote schaal, zonder dat men zich dat bewust is, gebeurt, is het zeer beeldend. Veronderstel een oplossing en er is géén probleem.
Waar het veronderstellen van een blikopener bij ieder gezond denkend mens als absurd wordt afgedaan, geldt dit in veel mindere mate bij “veronderstel een normale verdeling”.
Doorgaans is normaal zelden ‘normaal’
In mijn hoedanigheid van Directeur Operations vroeg ik ooit een jonge ambitieuze Industrial Engineer om zich te verdiepen in het aantal palletplaatsen dat wij in de fabriek nodig zouden hebben als we in de komende jaren onze strategische ambitie qua sales en productie waar zouden maken.
Na een intensieve studie en een enorm spreadsheet had hij berekend hoeveel palletplaatsen we de komende jaren nodig zouden hebben. Een spreadsheet geeft een illusie van accuraatheid.
Benieuwd naar zijn bevindingen vroeg ik hem om zijn aannames. Naar bleek was hij zonder te weten twee keer door rood gereden. Hij had aangenomen dat de jaarverkopen en productie gemiddeld over het jaar verdeeld zouden zijn, terwijl we een duidelijk seizoenspatroon hadden ten gevolge van de bouw. Daarnaast had hij aangenomen dat de voorraad (het product in wording) zich binnen de week gemiddeld door het bedrijf zou voortbewegen, terwijl er in de opeenvolgende bewerkingsplekken afdelingen waren die in dagdienst, twee ploegen, drie ploegen en tot slot de bottleneck in vijf ploegen werkten. Dus zelfs al zou de vraag normaal verdeeld zijn, dan nog leidt het verschil in capaciteit (een afdeling kan het werk in één ploeg, twee of drie ploegen af, of werkt continue in vijf ploegen) tot onevenredige ophopingen van voorraad in die fabriek gedurende de week.
Statistiek feitelijk vaak pas toepassen bij gebrek aan alternatief
De ervaring leert dat bij veel vraagstellingen, veel analyses, het veel handiger en gepaster is om te vragen, te bellen, te kijken, te experimenteren om op die wijze te kijken of er een oplossing voorhanden is in plaats van het antwoord te zoeken via statistische berekeningen.
Echter, we kunnen bij consumentenmarketing gezien de grote aantallen niet iedere consument ondervragen, noch kunnen we bij veel kwaliteitsmetingen van grootschalige processen de significantie zien en daar vormt de statistiek een fenomenaal krachtig middel. Alvorens statistiek ergens op los te laten is het wel enorm belangrijk om te kijken of we in mediocristan zitten en of er voldoende grote hoeveelheid waarnemingen voorhanden is.

Tot slot, zoals Godfried Bomans lang geleden al treffend verwoordde over hoe gevaarlijk het kan zijn om het gemiddelde kritiekloos toe te passen: “Een statisticus waadde eens een rivier door van gemiddeld een meter diep . . . hij verdronk!”
Veghel, augustus 2016